Probabilistic Programming in Turing.jl

Author

Mattias Villani

IID normal model

\[ X_1,\ldots,X_n \vert \mu, \sigma^2 \overset{iid}{\sim} N(\mu, \sigma^2) \]

Prior

\[ \sigma^2 \sim \chi^2(\nu_0, \sigma_0^2) \]

\[ \mu \vert \sigma^2 \sim N\Big(\mu_0, \frac{\sigma^2}{\kappa_0}\Big) \]

using Turing, Plots, LaTeXStrings

ScaledInverseChiSq(ν,τ²) = InverseGamma(ν/2,ν*τ²/2) # Scaled Inv-χ² distribution

# Setting up the Turing model:
@model function iidnormal(x, μ₀, κ₀, ν₀, σ²₀)
    σ² ~ ScaledInverseChiSq(ν₀, σ²₀)
    θ ~ Normal(μ₀, √(σ²/κ₀))  # prior
    n = length(x)  # number of observations
    for i in 1:n
        x[i] ~ Normal(θ, √σ²) # model
    end
end

# Set up the observed data
x = [15.77,20.5,8.26,14.37,21.09]

# Set up the prior
μ₀ = 20; κ₀ = 1; ν₀ = 5; σ²₀ = 5^2

# Settings of the Hamiltonian Monte Carlo (HMC) sampler.
α = 0.8
postdraws = sample(iidnormal(x, μ₀, κ₀, ν₀, σ²₀), NUTS(α), 10000, discard_initial = 1000)

p1 = histogram(postdraws.value[:,2], yaxis = false, title = L"\mu")
p2 = histogram(sqrt.(postdraws.value[:,1]), yaxis = false, title = L"\sigma")
plot(p1, p2, layout = (1,2), size = (600,300))

┌ Info: Found initial step size

└   ϵ = 0.2


Sampling:  11%|████▌                                    |  ETA: 0:00:01

Sampling:  21%|████████▋                                |  ETA: 0:00:01

Sampling:  30%|████████████▎                            |  ETA: 0:00:01

Sampling:  42%|█████████████████                        |  ETA: 0:00:01

Sampling:  52%|█████████████████████▌                   |  ETA: 0:00:01

Sampling:  64%|██████████████████████████               |  ETA: 0:00:00

Sampling:  74%|██████████████████████████████▍          |  ETA: 0:00:00

Sampling:  84%|██████████████████████████████████▋      |  ETA: 0:00:00

Sampling:  96%|███████████████████████████████████████▏ |  ETA: 0:00:00

Sampling: 100%|█████████████████████████████████████████| Time: 0:00:01

Poisson regression

\[ y_i \vert \boldsymbol{x}_i \sim\mathrm{Poisson}(\lambda_i) \\ \]

with log link

\[ \lambda_{i} =\exp(\boldsymbol{x}_{i}^{\top}\boldsymbol{\beta}) \]

and multivariate normal prior

\[ \boldsymbol{\beta} \sim N(\boldsymbol{0}, \tau^2 \boldsymbol{I}) \]

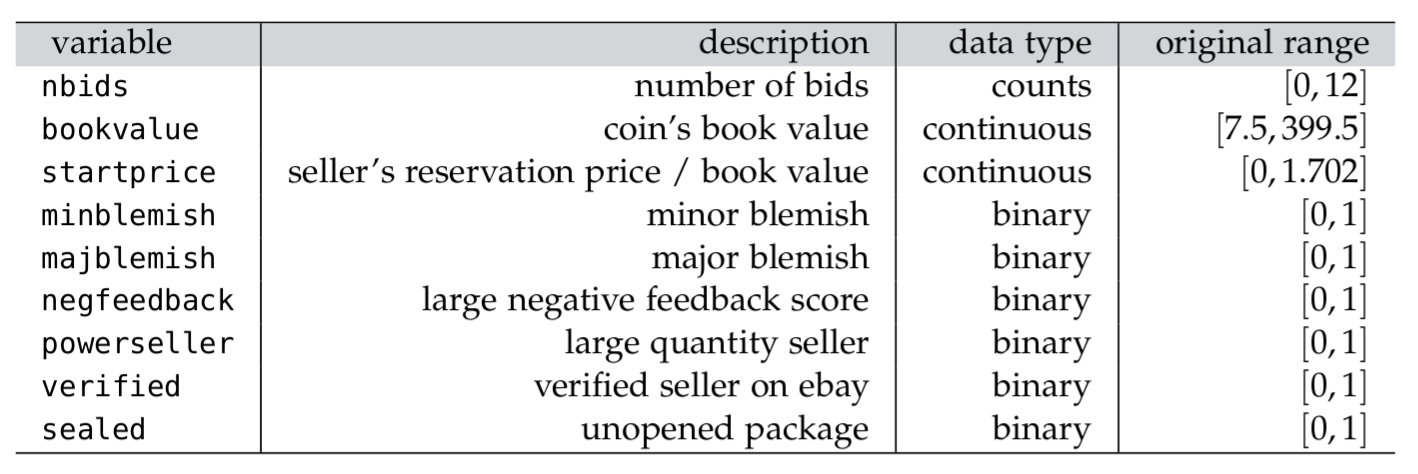
using Turing, CSV, Downloads, DataFrames, LinearAlgebra, LaTeXStrings, Plots

# Reading and transforming the eBay data
url = "https://github.com/mattiasvillani/BayesianLearningBook/raw/main/data/ebaybids/ebaybids.csv" 
df = CSV.read(Downloads.download(url), DataFrame)
n = size(df,1)
y = df[:,:NBidders]
X = [ones(n,1) log.(df.BookVal) .- mean(log.(df.BookVal)) df.ReservePriceFrac .- mean(df.ReservePriceFrac) df.MinorBlem df.MajorBlem  df.NegFeedback df.PowerSeller df.IDSeller df.Sealed]

varnames = ["intercept", "logbook", "startprice", "minblemish", "majblemish",    
      "negfeedback", "powerseller", "verified", "sealed"]

9-element Vector{String}:
 "intercept"
 "logbook"
 "startprice"
 "minblemish"
 "majblemish"
 "negfeedback"
 "powerseller"
 "verified"
 "sealed"

The Poisson regression with its prior is set up as Turing.jl using the @model macro:

# Setting up the poisson regression model
@model function poissonReg(y, X, τ)
    p = size(X,2)
    β ~ filldist(Normal(0, τ), p)  # all βⱼ are iid Normal(0, τ)
    λ = exp.(X*β)
    n = length(y)  
    for i in 1:n
        y[i] ~ Poisson(λ[i]) 
    end
end

poissonReg (generic function with 2 methods)

# HMC sampling from posterior
p = size(X, 2)
μ = zeros(p)    # Prior mean
τ = 10          # Prior standard deviation Σ = τ²I
α = 0.70        # target acceptance probability in NUTS sampler
model = poissonReg(y, X, τ)
chain = sample(model, NUTS(α), 10000, discard_initial = 1000, verbose = false)
rateratio = exp.(chain.value) # exp(β) is the incidence rate ratio

gr(grid = false)
h = []
for i = 1:p
    ptmp = histogram(rateratio[:,i], nbins = 50, fillcolor = :steelblue, linecolor = nothing, 
        normalize = true, title = varnames[i], xlab = L"\exp(\beta_{%$(i-1)})", 
        yaxis = false, fillopacity = 0.5, label = "")    
    push!(h, ptmp)
end
plot(h..., size = (600,600), legend = :right)

┌ Info: Found initial step size

└   ϵ = 2.9802322387695314e-9


Sampling:   2%|▋                                        |  ETA: 0:00:24

Sampling:   2%|▉                                        |  ETA: 0:00:26

Sampling:   2%|█                                        |  ETA: 0:00:25

Sampling:   3%|█▎                                       |  ETA: 0:00:25

Sampling:   4%|█▍                                       |  ETA: 0:00:25

Sampling:   4%|█▉                                       |  ETA: 0:00:24

Sampling:   6%|██▎                                      |  ETA: 0:00:22

Sampling:   6%|██▋                                      |  ETA: 0:00:21

Sampling:   8%|███▏                                     |  ETA: 0:00:20

Sampling:   8%|███▌                                     |  ETA: 0:00:19

Sampling:   9%|███▊                                     |  ETA: 0:00:19

Sampling:  10%|████▏                                    |  ETA: 0:00:19

Sampling:  10%|████▎                                    |  ETA: 0:00:19

Sampling:  11%|████▌                                    |  ETA: 0:00:19

Sampling:  12%|████▊                                    |  ETA: 0:00:19

Sampling:  12%|████▉                                    |  ETA: 0:00:19

Sampling:  12%|█████▏                                   |  ETA: 0:00:19

Sampling:  13%|█████▍                                   |  ETA: 0:00:19

Sampling:  14%|█████▌                                   |  ETA: 0:00:19

Sampling:  14%|█████▊                                   |  ETA: 0:00:19

Sampling:  14%|██████                                   |  ETA: 0:00:19

Sampling:  15%|██████▏                                  |  ETA: 0:00:18

Sampling:  16%|██████▍                                  |  ETA: 0:00:18

Sampling:  16%|██████▌                                  |  ETA: 0:00:18

Sampling:  16%|██████▊                                  |  ETA: 0:00:18

Sampling:  17%|███████                                  |  ETA: 0:00:18

Sampling:  18%|███████▏                                 |  ETA: 0:00:18

Sampling:  18%|███████▍                                 |  ETA: 0:00:18

Sampling:  19%|███████▊                                 |  ETA: 0:00:18

Sampling:  20%|████████                                 |  ETA: 0:00:17

Sampling:  20%|████████▍                                |  ETA: 0:00:17

Sampling:  21%|████████▋                                |  ETA: 0:00:17

Sampling:  22%|████████▉                                |  ETA: 0:00:17

Sampling:  22%|█████████                                |  ETA: 0:00:17

Sampling:  23%|█████████▍                               |  ETA: 0:00:17

Sampling:  24%|█████████▉                               |  ETA: 0:00:16

Sampling:  24%|██████████                               |  ETA: 0:00:16

Sampling:  26%|██████████▌                              |  ETA: 0:00:16

Sampling:  26%|██████████▋                              |  ETA: 0:00:16

Sampling:  26%|██████████▉                              |  ETA: 0:00:16

Sampling:  27%|███████████▏                             |  ETA: 0:00:16

Sampling:  28%|███████████▌                             |  ETA: 0:00:16

Sampling:  28%|███████████▋                             |  ETA: 0:00:15

Sampling:  30%|████████████▏                            |  ETA: 0:00:15

Sampling:  30%|████████████▌                            |  ETA: 0:00:15

Sampling:  31%|████████████▊                            |  ETA: 0:00:15

Sampling:  32%|████████████▉                            |  ETA: 0:00:15

Sampling:  32%|█████████████▍                           |  ETA: 0:00:14

Sampling:  34%|█████████████▊                           |  ETA: 0:00:14

Sampling:  34%|██████████████                           |  ETA: 0:00:14

Sampling:  35%|██████████████▍                          |  ETA: 0:00:14

Sampling:  36%|██████████████▌                          |  ETA: 0:00:14

Sampling:  36%|███████████████                          |  ETA: 0:00:13

Sampling:  37%|███████████████▏                         |  ETA: 0:00:13

Sampling:  38%|███████████████▋                         |  ETA: 0:00:13

Sampling:  38%|███████████████▊                         |  ETA: 0:00:13

Sampling:  40%|████████████████▎                        |  ETA: 0:00:13

Sampling:  40%|████████████████▍                        |  ETA: 0:00:13

Sampling:  41%|████████████████▊                        |  ETA: 0:00:13

Sampling:  42%|█████████████████                        |  ETA: 0:00:12

Sampling:  42%|█████████████████▎                       |  ETA: 0:00:12

Sampling:  42%|█████████████████▍                       |  ETA: 0:00:12

Sampling:  43%|█████████████████▋                       |  ETA: 0:00:12

Sampling:  44%|█████████████████▉                       |  ETA: 0:00:12

Sampling:  44%|██████████████████▎                      |  ETA: 0:00:12

Sampling:  45%|██████████████████▌                      |  ETA: 0:00:12

Sampling:  46%|██████████████████▋                      |  ETA: 0:00:12

Sampling:  46%|██████████████████▉                      |  ETA: 0:00:12

Sampling:  47%|███████████████████▎                     |  ETA: 0:00:11

Sampling:  48%|███████████████████▌                     |  ETA: 0:00:11

Sampling:  48%|███████████████████▋                     |  ETA: 0:00:11

Sampling:  49%|████████████████████▏                    |  ETA: 0:00:11

Sampling:  50%|████████████████████▌                    |  ETA: 0:00:11

Sampling:  51%|████████████████████▉                    |  ETA: 0:00:10

Sampling:  52%|█████████████████████▏                   |  ETA: 0:00:10

Sampling:  52%|█████████████████████▍                   |  ETA: 0:00:10

Sampling:  53%|█████████████████████▊                   |  ETA: 0:00:10

Sampling:  54%|█████████████████████▉                   |  ETA: 0:00:10

Sampling:  54%|██████████████████████▏                  |  ETA: 0:00:10

Sampling:  55%|██████████████████████▌                  |  ETA: 0:00:10

Sampling:  56%|██████████████████████▊                  |  ETA: 0:00:09

Sampling:  56%|███████████████████████                  |  ETA: 0:00:09

Sampling:  56%|███████████████████████▏                 |  ETA: 0:00:09

Sampling:  57%|███████████████████████▍                 |  ETA: 0:00:09

Sampling:  58%|███████████████████████▋                 |  ETA: 0:00:09

Sampling:  58%|████████████████████████                 |  ETA: 0:00:09

Sampling:  59%|████████████████████████▎                |  ETA: 0:00:09

Sampling:  60%|████████████████████████▍                |  ETA: 0:00:09

Sampling:  60%|████████████████████████▋                |  ETA: 0:00:08

Sampling:  60%|████████████████████████▊                |  ETA: 0:00:08

Sampling:  61%|█████████████████████████                |  ETA: 0:00:08

Sampling:  62%|█████████████████████████▎               |  ETA: 0:00:08

Sampling:  62%|█████████████████████████▋               |  ETA: 0:00:08

Sampling:  63%|█████████████████████████▉               |  ETA: 0:00:08

Sampling:  64%|██████████████████████████               |  ETA: 0:00:08

Sampling:  64%|██████████████████████████▎              |  ETA: 0:00:08

Sampling:  65%|██████████████████████████▋              |  ETA: 0:00:07

Sampling:  66%|██████████████████████████▉              |  ETA: 0:00:07

Sampling:  66%|███████████████████████████              |  ETA: 0:00:07

Sampling:  67%|███████████████████████████▌             |  ETA: 0:00:07

Sampling:  68%|███████████████████████████▉             |  ETA: 0:00:07

Sampling:  69%|████████████████████████████▎            |  ETA: 0:00:07

Sampling:  70%|████████████████████████████▌            |  ETA: 0:00:07

Sampling:  70%|████████████████████████████▊            |  ETA: 0:00:06

Sampling:  70%|████████████████████████████▉            |  ETA: 0:00:06

Sampling:  71%|█████████████████████████████▏           |  ETA: 0:00:06

Sampling:  72%|█████████████████████████████▍           |  ETA: 0:00:06

Sampling:  72%|█████████████████████████████▊           |  ETA: 0:00:06

Sampling:  74%|██████████████████████████████▏          |  ETA: 0:00:06

Sampling:  74%|██████████████████████████████▍          |  ETA: 0:00:06

Sampling:  74%|██████████████████████████████▌          |  ETA: 0:00:05

Sampling:  75%|██████████████████████████████▊          |  ETA: 0:00:05

Sampling:  76%|███████████████████████████████▏         |  ETA: 0:00:05

Sampling:  76%|███████████████████████████████▍         |  ETA: 0:00:05

Sampling:  77%|███████████████████████████████▋         |  ETA: 0:00:05

Sampling:  78%|███████████████████████████████▊         |  ETA: 0:00:05

Sampling:  78%|████████████████████████████████         |  ETA: 0:00:05

Sampling:  78%|████████████████████████████████▏        |  ETA: 0:00:05

Sampling:  79%|████████████████████████████████▍        |  ETA: 0:00:04

Sampling:  80%|████████████████████████████████▋        |  ETA: 0:00:04

Sampling:  80%|████████████████████████████████▊        |  ETA: 0:00:04

Sampling:  80%|█████████████████████████████████        |  ETA: 0:00:04

Sampling:  82%|█████████████████████████████████▍       |  ETA: 0:00:04

Sampling:  82%|█████████████████████████████████▋       |  ETA: 0:00:04

Sampling:  82%|█████████████████████████████████▉       |  ETA: 0:00:04

Sampling:  83%|██████████████████████████████████       |  ETA: 0:00:04

Sampling:  84%|██████████████████████████████████▎      |  ETA: 0:00:04

Sampling:  84%|██████████████████████████████████▌      |  ETA: 0:00:03

Sampling:  84%|██████████████████████████████████▋      |  ETA: 0:00:03

Sampling:  86%|███████████████████████████████████      |  ETA: 0:00:03

Sampling:  86%|███████████████████████████████████▌     |  ETA: 0:00:03

Sampling:  88%|███████████████████████████████████▉     |  ETA: 0:00:03

Sampling:  88%|████████████████████████████████████▏    |  ETA: 0:00:03

Sampling:  88%|████████████████████████████████████▎    |  ETA: 0:00:02

Sampling:  89%|████████████████████████████████████▌    |  ETA: 0:00:02

Sampling:  90%|████████████████████████████████████▊    |  ETA: 0:00:02

Sampling:  90%|████████████████████████████████████▉    |  ETA: 0:00:02

Sampling:  90%|█████████████████████████████████████▏   |  ETA: 0:00:02

Sampling:  92%|█████████████████████████████████████▌   |  ETA: 0:00:02

Sampling:  92%|█████████████████████████████████████▉   |  ETA: 0:00:02

Sampling:  93%|██████████████████████████████████████▏  |  ETA: 0:00:01

Sampling:  94%|██████████████████████████████████████▌  |  ETA: 0:00:01

Sampling:  94%|██████████████████████████████████████▊  |  ETA: 0:00:01

Sampling:  96%|███████████████████████████████████████▏ |  ETA: 0:00:01

Sampling:  96%|███████████████████████████████████████▋ |  ETA: 0:00:01

Sampling:  98%|████████████████████████████████████████ |  ETA: 0:00:01

Sampling:  98%|████████████████████████████████████████▏|  ETA: 0:00:00

Sampling:  98%|████████████████████████████████████████▍|  ETA: 0:00:00

Sampling:  99%|████████████████████████████████████████▊|  ETA: 0:00:00

Sampling: 100%|█████████████████████████████████████████| Time: 0:00:21

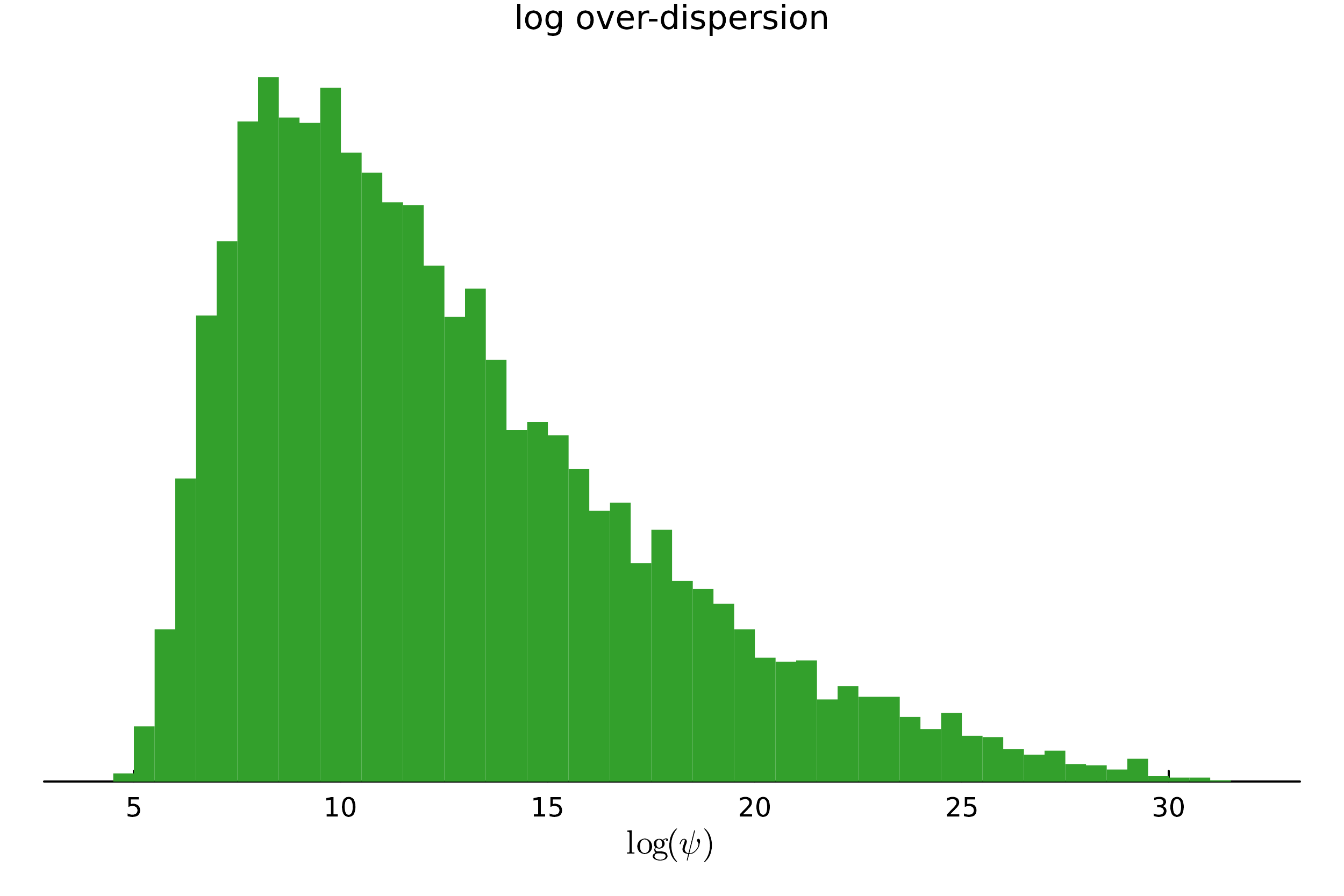
Extensions to more complex models is easy. Negative binomial regression

\[ y_{i}\vert\boldsymbol{x}_{i} \sim\mathrm{NegBinomial}\left(\psi,p=\frac{\psi}{\psi+\lambda_{i}}\right),\quad\lambda_{i}=\exp(\boldsymbol{x}_{i}^{\top}\boldsymbol{\beta}) \]

# Negative binomial regression 
@model function negbinomialReg(y, X, τ, μ₀, σ₀)
    p = size(X,2)
    β ~ filldist(Normal(0, τ), p)  # all βⱼ are iid Normal(0, τ)
    λ = exp.(X*β)
    ψ ~ LogNormal(μ₀, σ₀)             # log of overdispersion parameter
    n = length(y)  
    for i in 1:n
        y[i] ~ NegativeBinomial(ψ, ψ/(ψ + λ[i])) # mean is λ here, but var = λ(1 + λ/ψ) 
    end
end

μ₀ = 0   # Prior mean of log(ψ), where ψ is the overdispersion parameter
σ₀ = 10  
α = 0.70  # target acceptance probability in NUTS sampler
model = negbinomialReg(y, X, τ, μ₀, σ₀)
chain = sample(model, NUTS(α), 10000, discard_initial = 1000)
rateratio = exp.(chain.value)

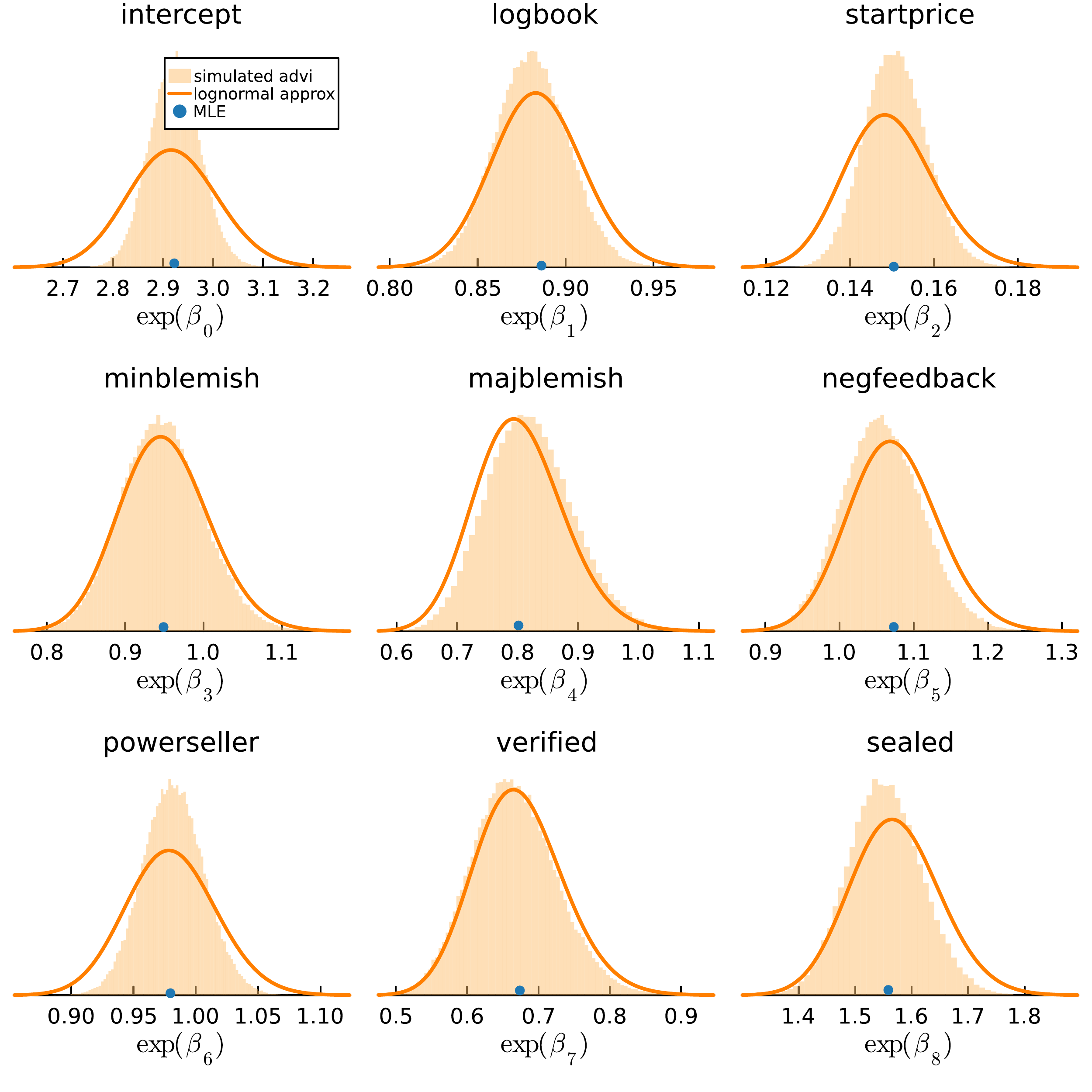
Variational inference in Turing.jl

# Variational inference assuming posterior is independent normals
nSamples = 10
nGradSteps = 1000
approx_post = vi(model, ADVI(nSamples, nGradSteps)) # error when I try it now.
approx_post.dist.m # mean of variational approximation
approx_post.dist.σ # stdev of variational approximation
βsample = rand(approx_post, 10000)